The Transformer Architecture: A Deep Dive

An intuition-first, reference-grade breakdown of every building block—from why attention was invented to how encoder, decoder, and encoder-decoder architectures work

NLP
Deep Learning
Author

Imad Dabbura

Published

February 14, 2023

Modified

November 8, 2025

Introduction


Figure 1: The vanilla Transformer model (source)

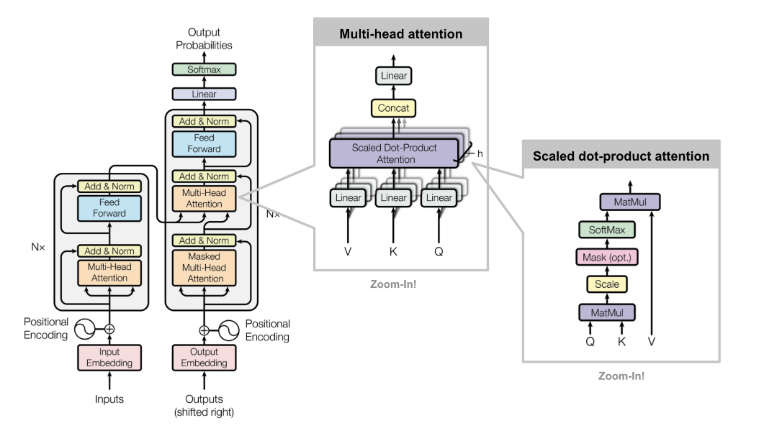
If you’ve called from transformers import BertModel or prompted GPT-4, you’ve used a Transformer. But what actually happens when it processes text? Why does attention use three separate projections — Q, K, and V? Why does the decoder need a causal mask? And how did a single 2017 translation paper become the foundation of essentially all modern AI?

The best way to answer these questions is to build one yourself — understanding the motivation behind every design choice before any code. In this post, we start with the problem that motivated the Transformer (sequential bottlenecks in RNNs), build the attention mechanism step by step, implement each component in PyTorch with annotated shapes, and assemble all three architecture variants from scratch.

By the end, you will be able to:

  1. Explain why each component exists, not just what it does
  2. Trace a forward pass through the full encoder-decoder architecture, step by step
  3. Understand the three architecture variants (encoder-only, decoder-only, encoder-decoder) and when to use each
  4. Read modern Transformer papers and recognize the improvements they describe

Roadmap: We will build up from first principles — starting with why RNNs fell short, then developing the attention mechanism from scratch, then adding each supporting component, and finally assembling the full architectures.

How to Use This Post

This post is designed as a reference as much as a read-through. Every major section is self-contained enough that you can jump to it when a concept isn’t clear. The section headers in the sidebar are your table of contents.

1. The Problem: Why Not RNNs?

To understand why the Transformer is designed the way it is, you first need to understand what it replaced — and what was fundamentally broken about it.

1.1 The RNN Mental Model

A Recurrent Neural Network processes a sequence one token at a time. After seeing each token \(w_t\), it updates a fixed-size hidden state \(h_t\) that is supposed to summarize everything the model has seen so far:

\[h_t = f(h_{t-1},\, w_t)\]

The hidden state is then passed to the next step. Think of it as a single notepad that a reader carries through a book, rewriting one paragraph of notes after each page. By the time they reach page 500, that notepad contains almost nothing from page 1 — there simply wasn’t room to preserve it through 499 rewrites.

This is not a metaphor for a failure mode; it is the fundamental architectural constraint. The RNN must compress all prior context into a fixed-size vector, and that compression is lossy by design.

1.2 The Long-Range Dependency Problem

Language is full of dependencies that span many tokens. Consider:

“The trophy didn’t fit in the suitcase because it was too large.”

To resolve what “it” refers to, a model must connect a pronoun near the end of the sentence back to a noun near the beginning. In an RNN, that connection must survive through every intermediate hidden state update. Each update potentially overwrites or dilutes the earlier information. The longer the sequence, the worse this gets.

1.3 The Vanishing Gradient Problem

The training-time failure mirrors the inference-time failure. When we backpropagate through an RNN, the gradient of the loss with respect to early hidden states is a product of Jacobians — one per time step:

\[\frac{\partial L}{\partial h_0} = \frac{\partial L}{\partial h_T} \prod_{t=1}^{T} \frac{\partial h_t}{\partial h_{t-1}}\]

If the entries of those Jacobians are consistently less than 1 (common with bounded activations like tanh), the product shrinks exponentially with \(T\). Gradients from the loss signal barely reach the early time steps, so the model cannot learn from long-range dependencies even if it wanted to.

LSTMs and GRUs mitigate this with gating mechanisms, but they don’t eliminate it — they just slow the decay. (For a full treatment of LSTMs and their gating solution, see the Inside LSTMs post.)

1.4 The Sequential Processing Bottleneck

RNNs are inherently sequential: you cannot compute \(h_t\) until you have \(h_{t-1}\). This makes it impossible to parallelize across the time dimension. For a sequence of length \(T\), the forward pass requires \(T\) sequential steps regardless of how many GPUs you have.

Modern GPUs are massively parallel processors — they shine on matrix multiplications that can be batched across thousands of operations simultaneously. RNNs waste almost all of that capacity.

The Three Failure Modes

RNNs fail in three compounding ways: (1) the hidden state bottleneck loses information over long sequences; (2) vanishing gradients prevent learning long-range relationships from the training signal; (3) sequential computation prevents parallelization, making training slow regardless of hardware. The Transformer addresses all three — not with patches, but by replacing sequential recurrence with a fundamentally different mechanism.

2. The Big Idea: Attention as Direct Communication

The central insight of the Transformer is deceptively simple: throw out sequential processing entirely and let every token communicate directly with every other token, in a single parallel operation.

2.1 From Sequential Relay to Direct Access

With an RNN, every relationship between tokens must be mediated through the hidden state — information travels through a long chain before it reaches its destination. With attention, every token asks every other token directly: “How relevant are you to me?” The answer shapes what information each token receives.

This is a fundamentally different computational paradigm: instead of routing information through a bottleneck, we create a direct, differentiable communication channel between all pairs of tokens simultaneously. The attention matrix for a sequence of length \(T\) is \(T \times T\) — every pair gets its own weight.

2.2 The Library Analogy: Query, Key, Value

The attention mechanism is most naturally understood as a soft database lookup.

Imagine walking into a library. You have a query in mind — say, you’re looking for books about long-range dependencies in sequences. Every book in the library has a key on its spine: a short descriptor of what’s inside. You compare your query against every key, computing a relevance score for each book. Then you retrieve the values — the actual content — weighted by those relevance scores. The most relevant books contribute the most to what you walk away knowing.

This is exactly what the Transformer’s attention mechanism does at every layer, for every token:

  • Query (\(Q\)): what this token is looking for
  • Key (\(K\)): what this token offers to match against
  • Value (\(V\)): what this token actually communicates if attended to

The attended output for each token is a weighted mixture of all value vectors, where the weights are determined by the similarity between that token’s query and all other tokens’ keys.

The Key Insight

Attention is not a neural network layer in the traditional sense — it is a soft, differentiable database lookup. It is differentiable because the retrieval weights are produced by a smooth function (softmax), so gradients flow through the lookup operation during backpropagation. The queries, keys, and values are all learned — the model learns what to look for, what to advertise, and what to say.

We’ll return to this library analogy throughout — it explains why Q, K, and V need to be separate projections, and what the attention weights actually represent numerically.

2.3 Why This Architecture Generalizes Beyond Language

Here is the deeper insight that explains why Vision Transformers, AlphaFold2, audio Transformers, and point cloud Transformers all use the same architecture as BERT and GPT — often with almost no modification.

The Transformer has almost no structural inductive bias. CNNs assume that nearby pixels are related — they bake in locality and translation equivariance as a prior. RNNs assume sequential order — they process left-to-right by construction. The Transformer assumes nothing about the structure of its input beyond what the positional encoding tells it. Every pair of positions is treated symmetrically by the attention mechanism until the training data says otherwise.

This is simultaneously the weakness and the superpower:

  • Weakness: Without structural priors, the model needs more data to learn relationships that CNNs or RNNs would pick up for free. A CNN learns “adjacent pixels tend to be related” from very few examples; a Transformer must discover this from data.
  • Superpower: Any domain with a set of elements you want to relate to each other can be modeled by a Transformer. Images? Treat patches as tokens, inject 2D positional encodings (ViT). Proteins? Treat amino acids as tokens, use pairwise distances as positional information (AlphaFold2). Audio? Treat spectrogram frames as tokens. Graphs? Treat nodes as tokens.

The key insight: positional encoding is the only thing that changes across domains. The attention mechanism, FFN, LayerNorm, and residual connections are entirely domain-agnostic. Swap the positional encoding and the same architecture processes any structured data. This is why the Transformer became the universal architecture — not because it is uniquely suited to language, but because it is uniquely generic.

3. Tokenization: From Text to Numbers

Before anything else, raw text must be converted into numbers that the model can process. This conversion — tokenization — splits text into a vocabulary of subword units and maps each unit to an integer ID. The Transformer receives a B × T matrix of integers as input, where B is the batch size and T is the sequence length.

There are three families of tokenization strategy — character-level, word-level, and subword — each with distinct tradeoffs in vocabulary size, sequence length, and out-of-vocabulary handling. Modern language models universally use subword tokenization (BPE or WordPiece), which offers a vocabulary of tens of thousands of tokens while gracefully handling rare and novel words by decomposing them into known pieces.

This post focuses on the Transformer architecture that consumes tokenized sequences, not on tokenization itself. For a deep dive into how tokenization works:

  • Breaking Text Apart (The Smart Way) — covers all three strategies, the four-stage tokenization pipeline (normalization, pretokenization, subword model, postprocessing), WordPiece (BERT), and SentencePiece (LLaMA, XLM-R)
  • Byte Pair Encoding from Scratch — builds a BPE tokenizer from scratch, explains the training vs. encoding asymmetry, vocabulary size tradeoffs, and GPT-2’s regex pre-tokenization refinement

4. Embedding Layer

The embedding layer is the first thing the model does with the token IDs it receives. It has two jobs: turn integers into meaningful vectors, and inject positional information so the model knows where each token sits in the sequence.

4.1 Token Embeddings

An integer ID has no geometric structure. The number 42 is not “close to” 41 in any meaningful sense for language — the token at position 42 in the vocabulary might be completely unrelated to token 41. Neural networks need continuous-valued vectors they can do math on: compute dot products, measure distances, apply linear transformations.

A token embedding is a lookup table: a matrix of shape vocab_sz × embed_dim where each row is a learnable vector associated with one token. When the model sees token ID \(i\), it looks up row \(i\) and uses that vector downstream.

What makes embeddings powerful is that training forces semantically similar tokens into nearby regions of this vector space. After training on enough text, the embedding for “king” minus the embedding for “man” plus the embedding for “woman” lands close to “queen” — not because we encoded this relationship by hand, but because the training signal shaped the space that way.

An embedding turns a name tag into a GPS coordinate — suddenly you can measure distance, find neighbors, and do arithmetic.

Shape: B × T (integer IDs) → B × T × embed_dim (float vectors)

4.2 Positional Encodings

Here is the problem: attention is permutation equivariant. If you swap two rows of the input, the corresponding rows of the output swap identically. There is no mechanism inside the attention computation that cares about order. From the model’s perspective, “the cat sat on the mat” and “the mat sat on the cat” are identical sequences of tokens — just in different order.

To fix this, we add positional encodings to the token embeddings before feeding them into the Transformer. There are three main strategies:

Strategy 1: Sinusoidal Encodings (Original Paper)

The original Transformer paper uses fixed, non-learned positional encodings based on sine and cosine functions at different frequencies:

\[PE_{(pos,\, 2i)} = \sin\!\left(\frac{pos}{10000^{2i/d}}\right)\] \[PE_{(pos,\, 2i+1)} = \cos\!\left(\frac{pos}{10000^{2i/d}}\right)\]

The key insight: different frequency sinusoids create a unique “fingerprint” for each position. Think of it like reading a clock with multiple hands — the second hand, minute hand, and hour hand together identify a unique moment in time even though each hand alone is ambiguous. Low-frequency components (large denominator) vary slowly and encode coarse position (sentence-level); high-frequency components (small denominator) vary quickly and encode fine position (word-level). Together, every position from 0 to the maximum gets a unique encoding vector.

The advantage of sinusoidal encodings is that they can generalize to sequence lengths longer than those seen during training — the functions extend naturally to any position.

Strategy 2: Learned Absolute Encodings

Instead of fixing the positional encoding by formula, we can make it a learned parameter — another nn.Embedding table of shape max_seq_len × embed_dim. Each position from 0 to max_seq_len-1 gets its own learnable row, updated via backpropagation just like token embeddings.

This is what BERT and GPT use. The model learns what positional fingerprints work best for its task. The downside: sequences longer than max_seq_len seen during training have no positional encoding — the model has never learned what those positions mean.

Strategy 3: Rotary Positional Encoding (RoPE)

RoPE, introduced by Su et al. (2021) and used in LLaMA, Mistral, and GPT-NeoX, takes a fundamentally different approach: instead of adding a fixed vector to the embeddings, it rotates the query and key vectors by an angle proportional to their absolute position before computing the attention dot product.

The key property: when you rotate \(Q\) at position \(m\) and \(K\) at position \(n\), their dot product becomes a function of only the relative distance \(m - n\):

\[Q_m \cdot K_n = f(m - n)\]

This is highly desirable. Relative position — how far apart two tokens are — is often more informative than absolute position. Whether “cat” is token 5 or token 50 in the sentence matters less than how far it sits from the verb it modifies. RoPE bakes this directly into the attention computation at every layer, without requiring separate positional embedding vectors.

RoPE also generalizes better to longer sequences than the model was trained on, making it the dominant choice in modern open-source LLMs.

Implementation Note

The code below uses learned absolute positional embeddings — the simplest approach and standard for BERT-style encoder models. The embedding layer adds the token embedding and positional embedding, normalizes with LayerNorm, and applies dropout.

Code 
from dataclasses import dataclass
import torch
import torch.nn as nn
import torch.nn.functional as F
Code 
@dataclass
class TransformerConfig:
    vocab_sz: int = 1000
    block_sz: int = 8
    hidden_dropout_prob: float = 0.2
    num_attention_heads: int = 12
    num_hidden_layers: int = 6
    embed_dim: int = 768
    num_classes: int = 2
    layer_norm_eps: float = 1e-12
    intermediate_sz: int = 0  # set to 4 * embed_dim in __post_init__

    def __post_init__(self):
        if self.intermediate_sz == 0:
            self.intermediate_sz = 4 * self.embed_dim

config = TransformerConfig()
class Embeddings(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.token_embedding = nn.Embedding(config.vocab_sz, config.embed_dim)
        self.position_embedding = nn.Embedding(config.block_sz, config.embed_dim)
        self.layer_norm = nn.LayerNorm(config.embed_dim, eps=config.layer_norm_eps)
        self.dropout = nn.Dropout(p=0.1)

    def forward(self, x):
        ## x:              B x T  (integer token IDs)
        ## token_emb:      B x T x embed_dim
        ## position_emb:   T x embed_dim  (broadcast over batch)
        ## output:         B x T x embed_dim
        seq_len = x.shape[1]
        positions = torch.arange(seq_len, device=x.device)
        embeddings = self.token_embedding(x) + self.position_embedding(positions)
        embeddings = self.layer_norm(embeddings)
        return self.dropout(embeddings)
Code 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rcParams["figure.dpi"] = 150

def sinusoidal_pe(seq_len, d_model):
    pe  = np.zeros((seq_len, d_model))
    pos = np.arange(seq_len)[:, None]
    i   = np.arange(d_model)[None, :]
    div = 10000 ** (2 * (i // 2) / d_model)
    pe[:, 0::2] = np.sin(pos / div[:, 0::2])
    pe[:, 1::2] = np.cos(pos / div[:, 1::2])
    return pe

pe = sinusoidal_pe(seq_len=64, d_model=128)

fig, ax = plt.subplots(figsize=(10, 3.5))
img = ax.imshow(pe.T, cmap="RdBu_r", aspect="auto", vmin=-1, vmax=1)
ax.set_xlabel("Position in sequence", fontsize=12)
ax.set_ylabel("Embedding dimension", fontsize=12)
ax.set_title(
    "Sinusoidal Positional Encoding  —  each column is a unique position fingerprint",
    fontsize=11, pad=8
)
plt.colorbar(img, ax=ax, fraction=0.015, pad=0.02, label="Encoding value")
plt.tight_layout()
plt.savefig("positional-encoding-heatmap.png", dpi=150, bbox_inches="tight")
plt.show()
Figure 1: Sinusoidal positional encoding. Each column is a unique fingerprint for one position. Low-frequency components (bottom rows) vary slowly — encoding coarse, sentence-level position. High-frequency components (top rows) vary quickly — encoding fine, word-level position. Together, every position from 0 to max_seq_len gets a unique vector.

5. Scaled Dot-Product Attention

Attention is the core computation that makes everything else in the Transformer work. Everything up to this point — embeddings, positional encodings — has been preprocessing. This is the operation that enables direct token-to-token communication.

This section builds it up step by step: from the Q/K/V projections, through the dot-product similarity, scaling, softmax, and masking. By the end, the library analogy from Section 2 will have a precise mathematical form.

5.1 The Three Projections: Query, Key, Value

Given an input sequence \(x\) of shape B × T × embed_dim, we produce three separate linear projections:

\[Q = xW_Q, \quad K = xW_K, \quad V = xW_V\]

Each weight matrix (\(W_Q\), \(W_K\), \(W_V\)) has shape embed_dim × head_dim. These are learned parameters — different projection matrices produce different “perspectives” on the same input.

Why three separate projections instead of one? Because what a token wants (its query), what it offers to match against (its key), and what it actually communicates (its value) are three genuinely different things. Consider how a search engine works: your search query text (Q) is compared against the indexed keywords of a web page (K), but what you actually receive when you click is the full page content (V) — which may be organized completely differently from the index terms. Separating these three roles gives the model the flexibility to learn very different relationships for each.

5.2 Computing Attention Weights: A Worked Example

With Q, K, V in hand, the attention weights are computed as:

\[\text{weights} = \text{softmax}\!\left(\frac{QK^T}{\sqrt{d_k}}\right)\]

Let’s trace through this with a concrete 3-token example. Suppose our sequence is [“the”, “cat”, “sat”], with head_dim = 4. After the Q and K projections, imagine we have:

\[Q = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{bmatrix},\quad K = \begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 0 \end{bmatrix}\]

Step 1 — Dot products \(QK^T\) (shape 3 × 3): Every token’s query is dotted with every token’s key. The \((i,j)\) entry measures how much token \(i\) “wants” to attend to token \(j\).

\[QK^T = \begin{bmatrix} 1 & 1 & 2 \\ 1 & 1 & 0 \\ 1 & 2 & 2 \end{bmatrix}\]

Why dot products? Geometrically, the dot product of two vectors is large when they point in similar directions (small angle) and small when they are orthogonal. If a query and key are aligned — the token is “looking for” exactly what the other token “offers” — the dot product is high, and that token will receive a large attention weight.

Step 2 — Scale by \(\frac{1}{\sqrt{d_k}} = \frac{1}{2}\):

\[\frac{QK^T}{\sqrt{d_k}} = \begin{bmatrix} 0.5 & 0.5 & 1.0 \\ 0.5 & 0.5 & 0.0 \\ 0.5 & 1.0 & 1.0 \end{bmatrix}\]

Step 3 — Softmax row-wise (each row sums to 1):

\[\text{weights} = \begin{bmatrix} 0.27 & 0.27 & 0.46 \\ 0.33 & 0.33 & 0.33 \\ 0.21 & 0.39 & 0.39 \end{bmatrix}\]

Row 1 (token “the”): attends most strongly to “sat” (0.46). Row 2 (“cat”): distributes evenly. Row 3 (“sat”): attends most to “cat” and itself.

Step 4 — Multiply by V (shape 3 × head_dim): The output for each token is a weighted combination of all value vectors, with weights from the softmax step. Token “the” will receive a mix of all three value vectors, weighted 27%/27%/46%. The output is a contextualized representation — the same token in a different sentence would produce different weights and therefore a different output vector.

The Departure from Static Embeddings

Notice what just happened: the token “the” — which starts with a fixed embedding vector identical in every sentence — now has a representation shaped by the presence of “cat” and “sat.” Run the same token through a different sentence (“the table broke”), and it emerges from attention with a different output vector.

This is the fundamental departure from static word embeddings like word2vec or GloVe: those give every token a single, context-free vector that never changes. A Transformer gives every token a contextual representation — numerically different depending on what surrounds it. “bank” in “river bank” and “bank” in “bank account” start with the same embedding but diverge after attention. This is why Transformer-based representations are so dramatically better at tasks requiring word sense disambiguation, coreference resolution, and syntactic parsing.

5.3 Why Scale by \(\sqrt{d_k}\)?

This is one of those design choices that looks arbitrary until you understand the numerical reason behind it.

Q and K are both initialized as approximately unit-variance random vectors. When you compute their dot product across d_k dimensions, the result has variance equal to \(d_k\) (sum of d_k independent unit-variance terms). For a typical head_dim of 64, the raw dot products have standard deviation 8. For head_dim = 768, standard deviation 27.

Large-magnitude inputs to softmax cause a saturation problem. When one logit is much larger than the others, softmax approaches a one-hot distribution — almost all weight goes to one token, and gradients for every other position become negligibly small. The model can only learn from the one token it attends to, and ignores all the rest.

Dividing by \(\sqrt{d_k}\) rescales the dot products back to approximately unit variance, regardless of head_dim. Softmax then produces a diffuse distribution — not too concentrated, not too uniform — and gradients flow to all positions during training.

Without scaling, attention becomes a dictatorship: one token captures all the weight and the rest are ignored. Scaling preserves the democracy: every token can contribute to the output.

5.4 Softmax: Competition, Not Independence

Why use softmax and not sigmoid (or any other normalization)?

Sigmoid applied to each attention logit independently would allow a token to “attend highly to everyone” at the same time, with no trade-off. But attention should be selective: attending more to one token means attending less to others.

Softmax is a competitive normalization — its outputs sum to 1, so the weights form a probability distribution over the context window. Increasing attention to one token necessarily decreases attention to all others. This forces the model to make decisions about what is relevant rather than attending indiscriminately to everything.

5.5 Causal Masking (Decoder Only)

In a language model, the task is to predict the next token from all previous tokens. If the model can see token \(t+1\) while predicting token \(t\), that is data leakage — the model would just copy the future token rather than learning to predict it.

The Transformer prevents this with a causal mask: before applying softmax, all positions in the upper triangle of the \(T \times T\) attention weight matrix are set to \(-\infty\):

Position:    1    2    3    4
Token 1:    ✓   -∞   -∞   -∞
Token 2:    ✓    ✓   -∞   -∞
Token 3:    ✓    ✓    ✓   -∞
Token 4:    ✓    ✓    ✓    ✓

After softmax, \(-\infty\) becomes exactly 0. Token 1 can only attend to itself. Token 3 can attend to tokens 1, 2, and 3 but not 4. The mask enforces a strict information asymmetry: you can read anything in the past, but nothing in the future.

This is implemented by registering a lower-triangular buffer in the AttentionHead and calling masked_fill before softmax.

5.6 Self-Attention vs. Cross-Attention

Self-attention: Q, K, and V all come from the same input sequence \(x\). Every token attends to every other token within the same sequence. This is what the encoder uses (bidirectional) and the decoder uses for its first sublayer (causal).

Cross-attention: Q comes from one sequence (the decoder’s hidden state), while K and V come from a different sequence (the encoder’s output). The decoder “reads” the encoder’s representation of the source sequence. This is the mechanism that connects the two halves of an encoder-decoder model.

The generalization is worth stating explicitly: any two sequences can be related through cross-attention, simply by using one as the source of Q and the other as the source of K and V. This is the same operation that connects modalities in vision-language models (text queries attend to image patch keys/values), that lets perceiver architectures compress long inputs (a small set of learned query vectors attends to a large input), and that underlies virtually all multi-modal conditioning. Cross-attention is not a feature of encoder-decoder models — it is a universal conditioning primitive.

The full attention equation:

\[\text{Attention}(Q, K, V) = \text{softmax}\!\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]


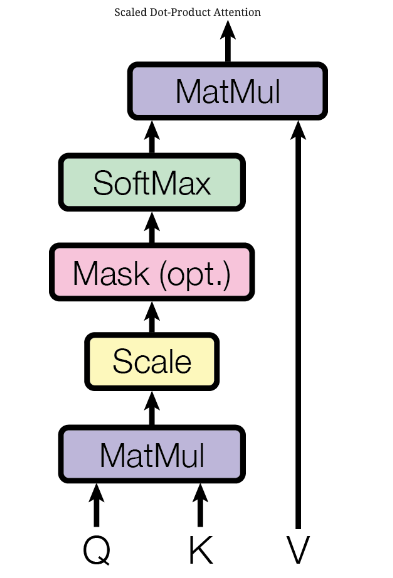
Figure 2: Scaled Dot-Product Attention (source)

5.7 The Quadratic Cost: Attention’s Fundamental Bottleneck

Computing attention requires forming the full \(T \times T\) weight matrix — every token’s query dotted against every token’s key. This is \(O(T^2 \cdot d_k)\) time and \(O(T^2)\) memory. For most sentences this is fine. For long documents, it becomes the dominant constraint:

Sequence length Attention matrix Memory (fp16, 1 head)
512 tokens 512 × 512 = 262K ~0.5 MB
4,096 tokens 4K × 4K = 16.8M ~32 MB
128K tokens 128K × 128K = 16.4B ~31 GB

This quadratic growth is why early BERT was capped at 512 tokens, why getting GPT-3 to handle long documents required tricks, and why an entire subfield of efficient attention exists — sliding-window attention (Longformer), linear attention, sparse attention (BigBird), and state-space models like Mamba are all attempts to approximate or restructure the \(T \times T\) computation to grow linearly with sequence length.

FlashAttention Changes the Hardware Utilization, Not the Complexity

FlashAttention (Dao et al., 2022) is often described as “making attention faster.” What it actually does: reorders the computation to tile through the attention matrix in blocks that fit in GPU SRAM (fast memory), avoiding slow round-trips to HBM (GPU global memory). The FLOPs are identical to standard attention; the memory bandwidth cost drops dramatically — 2–4× wall-clock speedup with numerically identical outputs. It also reduces peak memory from \(O(T^2)\) to \(O(T)\) by never materializing the full attention matrix. This is why FlashAttention is the standard in every modern training stack, but it does not fix the fundamental quadratic scaling problem for very long contexts.

class AttentionHead(nn.Module):
    def __init__(self, config, head_dim, is_decoder=False) -> None:
        super().__init__()
        self.q = nn.Linear(config.embed_dim, head_dim, bias=False)
        self.k = nn.Linear(config.embed_dim, head_dim, bias=False)
        self.v = nn.Linear(config.embed_dim, head_dim, bias=False)
        self.is_decoder = is_decoder
        if self.is_decoder:
            self.register_buffer(
                "mask", torch.tril(torch.ones(config.block_sz, config.block_sz))
            )

    def forward(self, query, key, value):
        ## query: B x T_q x embed_dim  (source of queries)
        ## key:   B x T_k x embed_dim  (source of keys)
        ## value: B x T_k x embed_dim  (source of values)
        q = self.q(query)  ## B x T_q x head_dim
        k = self.k(key)    ## B x T_k x head_dim
        v = self.v(value)  ## B x T_k x head_dim
        ## w: B x T_q x T_k  — pairwise similarity between every query and every key
        w = q @ k.transpose(2, 1) / (k.shape[-1] ** 0.5)
        if self.is_decoder:
            T = w.shape[-1]
            w = w.masked_fill(self.mask[:T, :T] == 0, -float("inf"))
        w = F.softmax(w, dim=-1)
        ## output: B x T_q x head_dim
        return w @ v
## Worked numerical example — Scaled Dot-Product Attention
## Sequence: ["the", "cat", "sat"], head_dim = 4

T, d_k = 3, 4

## Simulated Q and K projections (in practice these come from learned linear layers)
Q = torch.tensor([[1., 0, 1, 0],
                  [0., 1, 0, 1],
                  [1., 1, 0, 0]])  ## 3 x 4

K = torch.tensor([[1., 0, 0, 1],
                  [0., 1, 1, 0],
                  [1., 1, 0, 0]])  ## 3 x 4

torch.manual_seed(0)
V = torch.randn(T, d_k)           ## 3 x 4

## Step 1: raw dot products QK^T
scores = Q @ K.T
print(f"Step 1 — QK^T (shape {scores.shape}):\n{scores}\n")

## Step 2: scale by 1/√d_k
scores_scaled = scores / (d_k ** 0.5)
print(f"Step 2 — Scaled by 1/√{d_k} ≈ {1/d_k**0.5:.3f}:\n{scores_scaled.round(decimals=3)}\n")

## Step 3: softmax — turns scores into a probability distribution per query
weights = F.softmax(scores_scaled, dim=-1)
print(f"Step 3 — Attention weights (each row sums to 1):\n{weights.round(decimals=3)}")
print(f"Row sums: {weights.sum(dim=-1)}\n")

## Step 4: weighted sum of value vectors
output = weights @ V
print(f"Step 4 — Output = weights @ V  (shape {output.shape}):\n{output.round(decimals=3)}")
print("\nRow i of output is a context-aware mix of all value vectors,")
print("weighted by how much token i attends to each other token.")
Code 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rcParams["figure.dpi"] = 150

tokens  = ["the", "cat", "sat"]
weights = np.array([
    [0.27, 0.27, 0.46],   # "the" attends most to "sat"
    [0.33, 0.33, 0.33],   # "cat" distributes evenly
    [0.21, 0.39, 0.39],   # "sat" attends most to "cat" and itself
])

fig, ax = plt.subplots(figsize=(4.5, 3.8))
im = ax.imshow(weights, cmap="Blues", vmin=0, vmax=0.55)
ax.set_xticks(range(3))
ax.set_yticks(range(3))
ax.set_xticklabels(tokens, fontsize=13)
ax.set_yticklabels(tokens, fontsize=13)
ax.set_xlabel("Attends to  →  (Key)", fontsize=11)
ax.set_ylabel("Query token", fontsize=11)
ax.set_title("Attention weights  —  single head\n(each row sums to 1)", fontsize=11, pad=8)

for i in range(3):
    for j in range(3):
        ax.text(
            j, i, f"{weights[i, j]:.2f}",
            ha="center", va="center", fontsize=13,
            color="white" if weights[i, j] > 0.38 else "#222222",
            fontweight="bold"
        )

plt.colorbar(im, ax=ax, fraction=0.046, pad=0.04, label="Attention weight")
plt.tight_layout()
plt.savefig("attention-heatmap.png", dpi=150, bbox_inches="tight")
plt.show()
Figure 2: Attention weights for the [‘the’, ‘cat’, ‘sat’] example. Rows are query tokens; columns are keys. Each row is a probability distribution — how much each token attends to every other token.

6. Multi-Head Attention

6.1 Why Multiple Heads?

A single attention head learns one type of relationship between tokens. For example, it might learn to focus on the syntactic subject of a sentence whenever any token is processed — a subject-finding head. But language has many simultaneous relationship types that are all relevant at once:

  • Syntactic: subject-verb agreement, noun-adjective agreement
  • Semantic: coreference (“it” → “the trophy”), negation scope
  • Structural: attending to nearby tokens for local context
  • Task-specific: attending to sentiment-bearing words for classification

Multiple heads allow the model to learn all of these in parallel. Each head has its own independent weight matrices \(W_Q^h\), \(W_K^h\), \(W_V^h\) that project the same input \(x\) into a different lower-dimensional subspace:

\[\text{head\_dim} = \frac{\text{embed\_dim}}{\text{num\_heads}}\]

This subspace separation is the mechanism that makes specialization both possible and stable. Head 3’s attention weights are determined by \(W_Q^3 \cdot W_K^3\) inner products, which have nothing to do with what \(W_Q^7 \cdot W_K^7\) computes for head 7. Because they project into orthogonal subspaces of the embedding, heads don’t interfere with each other — a coreference head and a subject-finding head can coexist without one corrupting the other.

Empirical findings from BERTology (Clark et al., 2019) confirm that this specialization emerges after training: some heads consistently track syntactic dependencies across the entire network; others attend primarily to adjacent tokens, effectively implementing a local sliding window; some heads in BERT-style models attend heavily to the [SEP] token — a kind of “no-op” head that routes excess attention somewhere harmless when no strong relationship exists.

Importantly, this specialization is not designed in. It arises entirely from the training signal. The architecture only provides the capacity for parallel, independent subspace projections; training discovers what each subspace should track.


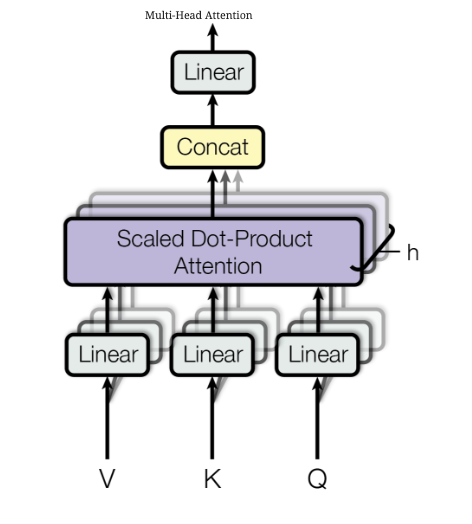
Figure 3: Multi-Head Attention with several attention layers running in parallel (source)

6.2 Implementation: Parallel Heads, Final Projection

Each head produces an output of shape B × T × head_dim. All heads run entirely in parallel — there is no communication between heads during the forward pass. The outputs of all heads are concatenated along the last dimension: num_heads × head_dim = embed_dim. The concatenated tensor then passes through a final linear projection \(W_O\) of shape embed_dim × embed_dim.

Why the final projection? The heads operated in isolation — each found something different in its own subspace. The \(W_O\) projection is the first opportunity for the model to mix information across heads: to combine what the coreference head found with what the subject-finding head found into a single coherent output vector.

Pedagogical vs. Efficient Implementation

The implementation below uses a Python loop over heads for clarity. In practice, all heads are computed in a single batched matrix multiply by reshaping the input to B × T × num_heads × head_dim and transposing — this is the approach used in production (and in torch.nn.MultiheadAttention). The pedagogical loop is equivalent but slower.

However, there is still a problem: multi-head attention is a weighted averaging operation — it is linear in V. Stacking multiple attention layers with nothing in between collapses to a single linear transformation. The network needs nonlinearity. That is the feed-forward network’s job.

class MultiHeadAttention(nn.Module):
    def __init__(self, config, is_decoder=False) -> None:
        super().__init__()
        head_dim = config.embed_dim // config.num_attention_heads
        self.heads = nn.ModuleList(
            [
                AttentionHead(config, head_dim, is_decoder)
                for _ in range(config.num_attention_heads)
            ]
        )
        ## Final projection mixes information across heads: embed_dim -> embed_dim
        self.output_proj = nn.Linear(config.embed_dim, config.embed_dim)

    def forward(self, query, key, value):
        ## query: B x T_q x embed_dim
        ## key:   B x T_k x embed_dim
        ## value: B x T_k x embed_dim
        ## Each head produces B x T_q x head_dim; cat gives B x T_q x embed_dim
        x = torch.cat([head(query, key, value) for head in self.heads], dim=-1)
        return self.output_proj(x)  ## B x T_q x embed_dim

7. Feed-Forward Network

7.1 Why Is It Needed?

Attention is a weighted averaging operation. It is linear in V: the output for each position is a linear combination of value vectors, where the combination weights come from the attention scores. If we stacked multiple attention layers with no nonlinearity in between, the composition of linear operations would remain linear — effectively equivalent to a single layer.

This is the same reason we use activation functions between layers in any neural network: without them, depth buys us nothing.

The feed-forward network (FFN) adds the essential nonlinearity. It processes each token’s representation independently after the attention layer. There is no mixing of tokens in the FFN — that is attention’s job. The clean separation of concerns is intentional:

  • Attention: mixes information across positions (who talks to whom)
  • FFN: transforms each position’s representation non-linearly (what to say)

The FFN as a knowledge store. Research by Geva et al. (2021) provides a compelling interpretation: FFN layers function as associative memories. The first linear layer acts as a set of keys that pattern-match against the input; the second linear layer acts as the corresponding values that are retrieved and output. Most of a Transformer’s factual knowledge — the associations between entities, relations, and attributes — is hypothesized to live in FFN weights, not in the attention matrices.

Attention is the routing system. The FFN is the knowledge store.

7.2 Architecture Details

The FFN has a characteristic structure: expand, activate, contract.

  1. Expand: Linear projection from embed_dim → 4 × embed_dim. The 4× factor is empirical — found to work well across a range of model sizes. The expanded intermediate dimension is where most of the model’s representational capacity lives, and it is the dimension that is typically scaled up when making larger models.
  2. Activate: GELU (Gaussian Error Linear Unit) nonlinearity. Unlike ReLU, GELU applies a smooth, probabilistic gate proportional to the Gaussian CDF. Empirically, GELU consistently outperforms ReLU in Transformer training. Modern models (LLaMA, PaLM) use SwiGLU — a gated variant — which further improves performance.
  3. Contract: Linear projection from 4 × embed_dim → embed_dim, restoring the original dimension for the residual connection.

Why position-wise? The FFN applies the same learned transformation to every position independently and in parallel. There is no weight-sharing across positions within a layer, but the same weight matrices process every position. This is sometimes called a “position-wise” or “point-wise” feed-forward layer.

class FeedForwardNN(nn.Module):
    def __init__(self, config):
        super().__init__()
        ## Expand to 4x hidden dim, then contract back — most capacity lives here
        self.l1 = nn.Linear(config.embed_dim, config.intermediate_sz)
        self.l2 = nn.Linear(config.intermediate_sz, config.embed_dim)
        self.dropout = nn.Dropout(config.hidden_dropout_prob)

    def forward(self, x):
        ## x:        B x T x embed_dim
        ## after l1: B x T x intermediate_sz  (expand)
        ## after l2: B x T x embed_dim        (contract)
        return self.dropout(self.l2(F.gelu(self.l1(x))))

8. Layer Normalization

8.1 Why Normalize at All?

Deep networks have a training stability problem: as signals propagate through many layers, the distribution of activations tends to shift and grow — a phenomenon called internal covariate shift. Layers that receive wildly varying input distributions must constantly adjust their weights just to track the shifting scale, not to learn meaningful transformations. This wastes capacity and slows training.

Think of it as keeping the working range of each layer consistent. Without normalization, earlier layers can produce outputs 100× larger than what later layers expect — the later layers waste capacity on a bookkeeping problem rather than learning anything about language.

Normalization is the engineering fix: explicitly constrain activation distributions to zero mean and unit variance at key points in the network, keeping signals in a regime where gradients are well-behaved throughout training.

8.2 Batch Normalization vs. Layer Normalization

Batch Normalization (Ioffe & Szegedy, 2015) normalizes each feature across the batch dimension. This works well for CNNs on images but has two critical failure modes for sequence models:

  1. Small batches: with batch size 1, the batch mean and variance are undefined (or estimated from a single sample). Transformers are often trained with small batch sizes per GPU.
  2. Variable-length sequences: different positions in a batch may have very different activation statistics. Normalizing across a mixed batch conflates these.

Layer Normalization (Ba et al., 2016) normalizes across the feature dimension instead of the batch dimension:

\[y = \frac{x - \mathbb{E}[x]}{\sqrt{\text{Var}[x] + \epsilon}} \cdot \gamma + \beta\]

The mean and variance are computed independently for each example, over all features of that example. This makes LayerNorm completely independent of batch size — it works identically whether batch size is 1 or 1000.

Batch Norm Layer Norm
Normalizes over Batch dimension Feature dimension
Running statistics for inference Yes No
Breaks for batch_size = 1 Yes No
Variable-length sequences Awkward Natural
Common in CNNs, image models Transformers, RNNs

The learnable parameters \(\gamma\) and \(\beta\): After normalization, every layer’s output would have zero mean and unit variance — too rigid. The learned scale (\(\gamma\)) and shift (\(\beta\)) let each layer restore whatever distribution works best for its downstream computation. Without them, normalization would over-constrain the model.

8.3 Pre-Norm vs. Post-Norm: A Critical Implementation Choice

The original Transformer paper placed LayerNorm after the residual addition (Post-LayerNorm). GPT-2 and virtually every modern large model places it before (Pre-LayerNorm). This seemingly minor change has significant consequences for training stability.

graph LR
    subgraph PostLN["Post-LN (original paper)"]
        A1[x] --> B1[Sublayer]
        A1 --> C1[+]
        B1 --> C1
        C1 --> D1[LayerNorm]
        D1 --> E1[output]
    end
    subgraph PreLN["Pre-LN (GPT-2, modern default)"]
        A2[x] --> B2[LayerNorm]
        B2 --> C2[Sublayer]
        A2 --> D2[+]
        C2 --> D2
        D2 --> E2[output]
    end

Post-LayerNorm (left) vs Pre-LayerNorm (right). Modern models use Pre-LN.

Post-LN: LN(x + sublayer(x)) Pre-LN: x + sublayer(LN(x))
Gradient path Normalization sits outside the residual — gradients must pass through it Normalization is inside — clean gradient highway through the residual
Training stability Sensitive; requires careful learning rate warm-up; can diverge More stable; trains without warm-up
Final performance Marginally better with enough tuning Slightly lower ceiling, but much easier to train

Modern practice defaults to Pre-LN: training stability at scale is worth more than marginal final performance differences. If you are building a new model, use Pre-LN.

9. Skip (Residual) Connections

9.1 The Residual Stream Mental Model

Think of a Transformer as a residual stream — a river of information that flows from the input through all the layers to the output. Each layer (attention + FFN) reads from the stream and writes a correction back to it via addition:

\[x_{\text{out}} = x_{\text{in}} + \text{sublayer}(x_{\text{in}})\]

No single layer “owns” the representation. Each layer adds its contribution to a shared river. The residual stream at any point contains the sum of everything all previous layers have written.

This framing — developed in mechanistic interpretability research — makes it immediately clear why attention heads can specialize: each head contributes independently and additively to the stream. They don’t compete or overwrite each other; they contribute independently, and the stream accumulates all contributions.

9.2 Why Residual Connections Work

Gradient highways. When backpropagating through \(y = x + F(x)\):

\[\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot \left(1 + \frac{\partial F}{\partial x}\right)\]

The term \(\frac{\partial L}{\partial y}\) reaches \(x\) directly, through the identity path — regardless of what \(F(x)\) does. Even if \(F\) has saturated activations or near-zero gradients, the loss signal still flows back to earlier layers. This is why ResNets with skip connections can be trained to hundreds of layers while the same architecture without them fails beyond a dozen.

Loss landscape smoothing. He et al. (2016) visualized the loss surfaces of deep networks with and without skip connections. Without them: chaotic, sharp, with many high-curvature local minima that trap gradient descent. With them: smooth, convex, much more navigable.


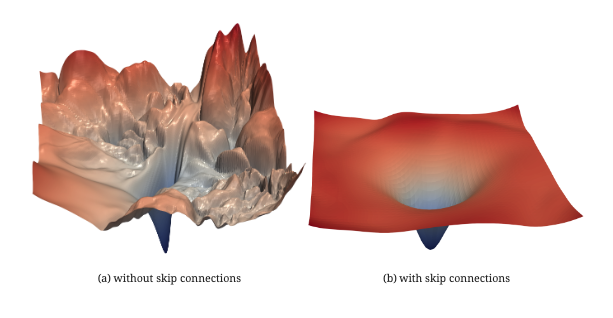
Figure 4: Loss surfaces of ResNet-56 with/without skip connections (source)

The forgetting argument. Without skip connections, each layer must preserve all useful information from its input in its output — if the layer wants to pass something unchanged, it must learn to do so explicitly. With skip connections, the default is identity — the layer only needs to learn what to add, not what to keep. This dramatically reduces the effective depth that the gradient must overcome.

However, training deep networks reliably requires one more ingredient beyond gradient highways — preventing the network from memorizing noise. That is dropout’s job.

10. Dropout

Dropout (Srivastava et al., 2014) randomly zeros a fraction p of activations during training. Each training step uses a different random mask, forcing the model not to rely on any particular activation path — a phenomenon called co-adaptation prevention.

The regularization effect comes from two mechanisms:

  1. Network size reduction: Dropping units creates a smaller effective network per step. A smaller network has fewer parameters to overfit.
  2. Implicit ensembling: Each step trains a different subnetwork. At inference, the full network approximates averaging over all these subnetworks — equivalent to a cheap bagging ensemble.

In Transformers, dropout is applied after the embedding layer (after adding token + positional embeddings), after each attention sublayer, and after each FFN sublayer.

Modern Large Models Often Skip Dropout

LLaMA, Mistral, and other recent large models use no dropout at all. At sufficient scale with enough data, the regularization effect of dropout is less necessary, and it slows training. Dropout remains important for smaller models trained on limited data, and for fine-tuning where overfitting is a risk.


Figure 5: Left: standard neural net. Right: thinned net after applying dropout — crossed units are dropped. (source)

With all the individual components understood — attention, FFN, LayerNorm, skip connections, dropout — it’s time to see how they snap together into a complete layer.

11. Assembling the Encoder Layer

Now that we have all the building blocks, let us see how they snap together into a single encoder layer — the repeated unit that makes up the encoder stack.

An encoder layer applies two sublayers in sequence, each wrapped in a residual connection and LayerNorm. Tracing the shapes at every step (using Pre-LN convention):

input:              B × T × embed_dim
                         │
                    LayerNorm(x)        →  B × T × embed_dim
                         │
               Multi-Head Self-Attention →  B × T × embed_dim
                         │
               + residual (add input x) →  B × T × embed_dim
                         │
                    LayerNorm(x)        →  B × T × embed_dim
                         │
                 Feed-Forward Network   →  B × T × embed_dim
                         │
               + residual (add input x) →  B × T × embed_dim
                         │
output:             B × T × embed_dim

Every token’s representation enters with shape embed_dim. After the attention sublayer, it has been updated by attending to all other tokens — information has been mixed across positions. After the FFN sublayer, each position’s representation has been transformed nonlinearly — independently from all other positions.

An encoder layer does two things: (1) let tokens talk to each other via attention, then (2) let each token digest what it heard via the FFN.

A full encoder stacks \(N\) of these layers (typically 6–24). Each layer refines the representations further — early layers tend to capture surface-level patterns, later layers capture increasingly abstract semantic relationships.

Post-LN in the Code

The implementation below uses the Post-LayerNorm arrangement from the original paper: LN(x + sublayer(x)). The Pre-LN alternative is shown in comments. For new models, prefer Pre-LN.

class EncoderLayer(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.attn = MultiHeadAttention(config)
        self.ff = FeedForwardNN(config)
        self.layer_norm_1 = nn.LayerNorm(config.embed_dim)
        self.layer_norm_2 = nn.LayerNorm(config.embed_dim)

    def forward(self, x):
        ## x: B x T x embed_dim  (input and output shape are identical)
        ##
        ## Post-LayerNorm arrangement (original Transformer paper):
        x = self.layer_norm_1(x + self.attn(x, x, x))  ## bidirectional self-attention
        x = self.layer_norm_2(x + self.ff(x))
        ##
        ## Pre-LayerNorm alternative (GPT-2+, more stable — recommended for new models):
        ## x = x + self.attn(self.layer_norm_1(x), self.layer_norm_1(x), self.layer_norm_1(x))
        ## x = x + self.ff(self.layer_norm_2(x))
        return x  ## B x T x embed_dim
class TransformerEncoder(nn.Module):
    def __init__(self, config) -> None:
        super().__init__()
        self.embeddings = Embeddings(config)
        self.encoder_blocks = nn.Sequential(
            *[EncoderLayer(config) for _ in range(config.num_hidden_layers)]
        )

    def forward(self, x):
        ## x:    B x T  (integer token IDs)
        x = self.embeddings(x)        ## B x T x embed_dim
        return self.encoder_blocks(x)  ## B x T x embed_dim

12. Assembling the Decoder Layer

The decoder layer differs from the encoder in one critical way: it adds a cross-attention sublayer between the masked self-attention and the FFN. This is the mechanism that lets the decoder read the encoder’s output.

A decoder layer applies three sublayers:

input:              B × T_dec × embed_dim
                         │
               LayerNorm(x)              →  B × T_dec × embed_dim
                         │
         Masked Multi-Head Self-Attention →  B × T_dec × embed_dim
         (Q, K, V all from decoder input,
          with causal mask)
                         │
        + residual                       →  B × T_dec × embed_dim
                         │
               LayerNorm(x)              →  B × T_dec × embed_dim
                         │
         Cross-Attention                 →  B × T_dec × embed_dim
         (Q from decoder, K and V from
          encoder output)
                         │
        + residual                       →  B × T_dec × embed_dim
                         │
               LayerNorm(x)              →  B × T_dec × embed_dim
                         │
               Feed-Forward Network      →  B × T_dec × embed_dim
                         │
        + residual                       →  B × T_dec × embed_dim
                         │
output:             B × T_dec × embed_dim

Sublayer 1 — Masked self-attention: Decoder tokens attend to each other, but only to past and current positions (causal mask). This builds a contextualized representation of the target sequence generated so far.

Sublayer 2 — Cross-attention: The decoder’s hidden state becomes the query. The encoder’s final output provides the keys and values. Every decoder position can attend to all encoder positions — this is how the decoder “reads” the full source sequence at every generation step.

Sublayer 3 — FFN: Same position-wise transformation as in the encoder.

Note on the Code Below

The DecoderLayer shown uses only masked self-attention (no cross-attention sublayer). It is therefore suited for the decoder-only (GPT-style) architecture. Cross-attention is addressed in the Encoder-Decoder section.

class DecoderLayer(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.attn = MultiHeadAttention(config, is_decoder=True)
        self.ff = FeedForwardNN(config)
        self.layer_norm_1 = nn.LayerNorm(config.embed_dim)
        self.layer_norm_2 = nn.LayerNorm(config.embed_dim)

    def forward(self, x):
        ## x: B x T x embed_dim
        ## Masked self-attention: each token only attends to past and current positions
        x = self.layer_norm_1(x + self.attn(x, x, x))
        x = self.layer_norm_2(x + self.ff(x))
        return x  ## B x T x embed_dim
class TransformerDecoder(nn.Module):
    def __init__(self, config) -> None:
        super().__init__()
        self.embeddings = Embeddings(config)
        self.decoder_blocks = nn.Sequential(
            *[DecoderLayer(config) for _ in range(config.num_hidden_layers)]
        )

    def forward(self, x):
        ## x:    B x T  (integer token IDs)
        x = self.embeddings(x)         ## B x T x embed_dim
        return self.decoder_blocks(x)  ## B x T x embed_dim

13. Architecture Variants

The same building blocks support three distinct architectures, differing only in which sublayers are present and whether attention is masked. Here is the full comparison before diving into each:

Encoder-Only Decoder-Only Encoder-Decoder
Attention masking Bidirectional Causal Causal in decoder; bidirectional in encoder
Cross-attention No No Yes
Input → Output Text → hidden states Text → next token Source text → target text
Canonical task Classification, NER, embeddings Text generation, LM Translation, summarization
Examples BERT, RoBERTa, DistilBERT GPT, LLaMA, Mistral T5, BART, mT5

13.1 Encoder-Only Architecture

Encoder-only models use bidirectional self-attention — every token attends to every other token with no masking. This means the representation of each token is conditioned on the full context: tokens to the left and the right. Bidirectional context makes encoder-only models excellent at understanding tasks: text classification, named entity recognition, extractive question answering, and computing sentence embeddings.

Why bidirectional? Classification does not require generating new tokens — it requires understanding the full input. A model that sees the entire sentence simultaneously can build richer representations than one forced to read left-to-right.

How is it trained? BERT-style models are trained with Masked Language Modeling (MLM): 15% of tokens are randomly masked ([MASK]), and the model must predict the original token at each masked position. Because the model can see all tokens to the left and right of the mask, this forces it to build bidirectional representations.

Classification head. A special [CLS] token is prepended to every sequence before the encoder. The encoder’s output at the [CLS] position — encoder_output[:, 0, :] — serves as an aggregate representation of the full sequence. This vector is passed through a linear classification head to produce logits.

Why [CLS] and Not Mean Pooling?

BERT uses [CLS] because it is trained to aggregate sequence-level information during pretraining (next sentence prediction task). In practice, mean pooling over all token representations often performs equally well or better for downstream tasks. Modern models trained without NSP use mean pooling as the default.

class TransformerForSequenceClassification(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.encoder = TransformerEncoder(config)
        self.dropout = nn.Dropout(config.hidden_dropout_prob)
        self.classifier = nn.Linear(config.embed_dim, config.num_classes)

    def forward(self, x):
        ## x:              B x T  (integer token IDs)
        ## encoder output: B x T x embed_dim
        ## [CLS] vector:   B x embed_dim  (position 0 aggregates sequence meaning)
        ## logits:         B x num_classes
        cls_output = self.encoder(x)[:, 0, :]
        return self.classifier(self.dropout(cls_output))

13.2 Decoder-Only Architecture

Decoder-only models use causal self-attention — each token can only attend to itself and previous tokens. This is the natural architecture for language modeling: predicting the next token given all previous tokens.

Why causal? Generating text requires predicting one token at a time. If the model could see future tokens while predicting token \(t\), it would simply copy them. The causal mask enforces the constraint that prediction at position \(t\) uses only information from positions \(0, 1, \ldots, t\).

Autoregressive generation. At inference, the decoder generates text by repeating:

graph LR
    A["Input tokens
[BOS, t₁, t₂]"] --> B["Decoder
(causal attention)"]
    B --> C["LM head
(linear + softmax)"]
    C --> D["Next token
t₃"]
    D --> A

Autoregressive generation loop in decoder-only models.

  1. Feed current token sequence through the decoder
  2. Take the output at the last position → pass through the LM head (linear projection to vocab_sz, then softmax)
  3. Sample the next token from the resulting distribution
  4. Append the sampled token to the sequence and repeat

Sampling strategies control how token \(t+1\) is chosen from the distribution:

  • Greedy: always pick the highest-probability token. Fast but repetitive.
  • Top-k: sample from the top-\(k\) tokens by probability. Controls diversity.
  • Top-p (nucleus): sample from the smallest set of tokens whose cumulative probability exceeds \(p\). Adaptive — uses fewer options when one token is dominant.
  • Temperature: divide all logits by temperature \(\tau\) before softmax. \(\tau < 1\) sharpens the distribution (more confident); \(\tau > 1\) flattens it (more random).

KV caching: why inference is efficient. The loop as described implies re-computing attention over the full growing sequence at every step — which would scale as \(O(T^2)\) for a \(T\)-token generation. Production systems avoid this with a KV cache: the K and V tensors for all past positions are stored after their first computation and reused on every subsequent step. Only the new token’s Q needs to be computed; it attends to the cached K/V from all prior positions. Each generation step then costs \(O(T \cdot d)\) instead of \(O(T^2 \cdot d)\).

The KV cache is a first-class engineering constraint in LLM deployment. For a model with \(L\) layers, \(H\) heads, head dimension \(d_k\), and current sequence length \(T\), the cache requires \(2 \cdot L \cdot H \cdot d_k \cdot T\) values — for LLaMA-3 70B at 4K context in fp16, that is roughly 5 GB. This is precisely why Grouped Query Attention (GQA) exists: by sharing a single K/V head across multiple Q heads, the cache shrinks by a factor of num_heads / num_kv_heads — often 8×. Every major modern model (LLaMA 2/3, Mistral, Gemma) uses GQA for exactly this reason.

class GPT(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.decoder = TransformerDecoder(config)
        self.dropout = nn.Dropout(config.hidden_dropout_prob)
        ## Project from embed_dim to vocab_sz to get next-token logits
        self.lm_head = nn.Linear(config.embed_dim, config.vocab_sz, bias=False)

    def forward(self, x):
        ## x:       B x T  (integer token IDs)
        ## decoded: B x T x embed_dim
        ## logits:  B x T x vocab_sz  (next-token distribution at every position)
        x = self.dropout(self.decoder(x))
        return self.lm_head(x)
class CrossAttentionDecoderLayer(nn.Module):
    """Decoder layer with three sublayers:
    (1) masked causal self-attention, (2) cross-attention to encoder, (3) FFN.
    """
    def __init__(self, config):
        super().__init__()
        self.self_attn  = MultiHeadAttention(config, is_decoder=True)
        self.cross_attn = MultiHeadAttention(config, is_decoder=False)
        self.ff         = FeedForwardNN(config)
        self.layer_norm_1 = nn.LayerNorm(config.embed_dim)
        self.layer_norm_2 = nn.LayerNorm(config.embed_dim)
        self.layer_norm_3 = nn.LayerNorm(config.embed_dim)

    def forward(self, x, encoder_output):
        ## x:              B x T_dec x embed_dim
        ## encoder_output: B x T_enc x embed_dim
        ##
        ## 1. Masked self-attention — decoder tokens attend to each other causally
        x = self.layer_norm_1(x + self.self_attn(x, x, x))
        ## 2. Cross-attention — Q from decoder, K and V from encoder
        ##    Every decoder position can attend to all encoder positions
        x = self.layer_norm_2(x + self.cross_attn(x, encoder_output, encoder_output))
        ## 3. Position-wise FFN
        x = self.layer_norm_3(x + self.ff(x))
        return x  ## B x T_dec x embed_dim


class Seq2SeqTransformer(nn.Module):
    """Encoder-decoder Transformer for sequence-to-sequence tasks
    such as machine translation and summarization.
    """
    def __init__(self, config):
        super().__init__()
        self.encoder_embeddings = Embeddings(config)
        self.decoder_embeddings = Embeddings(config)
        self.encoder_blocks = nn.ModuleList(
            [EncoderLayer(config) for _ in range(config.num_hidden_layers)]
        )
        self.decoder_blocks = nn.ModuleList(
            [CrossAttentionDecoderLayer(config) for _ in range(config.num_hidden_layers)]
        )
        self.lm_head = nn.Linear(config.embed_dim, config.vocab_sz, bias=False)

    def encode(self, src):
        ## src: B x T_enc  →  B x T_enc x embed_dim
        x = self.encoder_embeddings(src)
        for block in self.encoder_blocks:
            x = block(x)
        return x  ## B x T_enc x embed_dim

    def decode(self, tgt, encoder_output):
        ## tgt:            B x T_dec
        ## encoder_output: B x T_enc x embed_dim
        x = self.decoder_embeddings(tgt)  ## B x T_dec x embed_dim
        for block in self.decoder_blocks:
            x = block(x, encoder_output)
        return x  ## B x T_dec x embed_dim

    def forward(self, src, tgt):
        ## src: B x T_enc  (source token IDs, e.g. English)
        ## tgt: B x T_dec  (target token IDs, e.g. German — teacher-forced during training)
        encoder_output = self.encode(src)                    ## B x T_enc x embed_dim
        decoder_output = self.decode(tgt, encoder_output)   ## B x T_dec x embed_dim
        return self.lm_head(decoder_output)                  ## B x T_dec x vocab_sz

13.3 Encoder-Decoder Architecture

The encoder-decoder (or “sequence-to-sequence”) architecture is the original Transformer from Vaswani et al. (2017). It is designed for tasks where both input and output are text sequences — particularly tasks where the input and output are structurally different, like machine translation or summarization.

The two-phase interpretation:

  • Encoder: reads the full source sequence with bidirectional attention and produces a rich, contextualized representation. Think of this as “understanding the source.”
  • Decoder: generates the target sequence token by token, conditioned on the encoder’s representation at every step. Think of this as “generating the target given the understanding.”

How cross-attention implements conditioning. At every decoder step, the cross-attention sublayer takes: - Queries from the decoder’s current hidden state: “What do I need from the source?” - Keys and Values from the encoder’s final output: “Here is everything in the source.”

Every decoder position attends to all encoder positions simultaneously. The model learns which parts of the source to focus on when generating each target token — the alignment between source and target.

When encoder-decoder vs. decoder-only? Encoder-decoder models are preferred when source and target are structurally different (e.g., English → German, document → summary). For tasks where both input and output are similar in format (e.g., open-domain conversation, code completion), decoder-only models have largely taken over — they are simpler to train and scale, and can handle both input and output within a single sequence by formatting the task as a text completion problem.

Notable encoder-decoder models: T5 (Text-to-Text Transfer Transformer), BART, mT5, NLLB.

14. End-to-End Forward Pass Walkthrough

Let’s trace a complete forward pass through an encoder-decoder Transformer to see how all the pieces compose. We’ll use a small example: translating the English sentence “The cat sat” into German.

Setup: batch size \(B = 1\), source length \(T_{enc} = 3\), embed_dim = 768, num_heads = 12, head_dim = 64.

Step 1 — Tokenize the source.

“The cat sat” → subword tokenizer → [2, 47, 193] (integer IDs)

Shape: 1 × 3 (integers)

Step 2 — Token embedding lookup.

Each integer is mapped to a 768-dimensional vector via the embedding table.

Shape: 1 × 3 → 1 × 3 × 768

Step 3 — Add positional encodings.

A positional encoding vector is added to each token’s embedding. The result encodes both what the token is (token embedding) and where it sits (positional encoding).

Shape: 1 × 3 × 768 (unchanged)

Step 4 — N encoder layers.

Each encoder layer applies two sublayers: - Multi-head self-attention: All 3 tokens attend to all 3 tokens. The \(3 × 3\) attention weight matrix (12 heads, each with its own \(3 × 3\) weights) is computed, and each token’s representation is updated as a weighted mix of all token values. - FFN: Each token’s updated representation passes through the 2-layer FFN independently.

Shape at every encoder layer: 1 × 3 × 768 (unchanged throughout)

After \(N\) encoder layers, each of the 3 token positions holds a deeply contextualized representation — the meaning of “cat” is now informed by the presence of “The” and “sat” in context.

Encoder output: 1 × 3 × 768 — this is what the decoder will attend to.

Step 5 — Decoder receives the start token.

Decoder input starts with a start-of-sequence token [BOS].

Shape: 1 × 1 → (after embedding) 1 × 1 × 768

Step 6 — N decoder layers.

Each decoder layer applies three sublayers:

  1. Masked self-attention: Only 1 token so far, so the \(1 × 1\) causal attention matrix is trivially “attend to self.” Shape: 1 × 1 × 768.

  2. Cross-attention: Q comes from the decoder hidden state (1 × 1 × 768). K and V come from the encoder output (1 × 3 × 768). Attention weights have shape 1 × 1 × 3 — the single decoder position attends to all 3 encoder positions. Output: 1 × 1 × 768.

  3. FFN: 1 × 1 × 768 processed position-wise.

Step 7 — LM head.

The decoder output at the final position (1 × 1 × 768) is projected to vocab_sz via a linear layer, then softmax gives a probability distribution over the vocabulary.

Shape: 1 × 1 × 768 → 1 × 1 × vocab_sz → sample token → e.g., "Die" (German “The”)

Step 8 — Autoregressive loop.

Append "Die" to the decoder input. Repeat Steps 6–7 with decoder input [BOS, "Die"] to generate the next token. Continue until [EOS] is sampled or the maximum length is reached.

The key insight from this walkthrough: the encoder runs once for the full source sequence. The decoder runs once per generated token, attending to the full encoder output (which never changes) at every step via cross-attention.

15. What Transformers Actually Learn

Understanding the architecture is one thing; understanding what trained Transformers actually compute is another. Here is a brief map of empirical findings.

15.1 Attention Head Specialization

Clark et al. (2019) systematically analyzed BERT’s attention patterns across all layers and heads and found striking specialization:

  • Syntactic dependency heads: Certain heads consistently attend from a token to its syntactic governor (the word it depends on), recovering dependency parse relationships with high accuracy — without ever being trained on parse labels.
  • Positional heads: Some heads attend predominantly to adjacent tokens (the previous or next token), implementing local sliding-window attention.
  • [SEP] heads: Many heads in middle layers attend heavily to [SEP] tokens. The interpretation: when no strong relationship exists, these heads use [SEP] as a “garbage collector” — routing excess attention somewhere harmless.

This specialization is emergent, not designed. It arises purely from the training signal on downstream tasks.

15.2 FFN Layers as Factual Memories

Geva et al. (2021) showed that FFN sublayers act as key-value memories. The first linear layer’s weight rows act as “keys” that activate on specific input patterns; the second linear layer’s corresponding columns act as “values” that are retrieved and output.

This framing explains where factual knowledge lives in a language model. When a model correctly completes “The Eiffel Tower is located in ___“, the relevant association (Eiffel Tower → Paris) is likely stored as a key-value pair in the FFN weights of one or more layers — not in the attention matrices.

15.3 Layer Depth and Abstraction

Probing classifiers — small models trained to predict linguistic properties from internal representations — consistently find that:

  • Early layers (1–4): Surface-level features — part-of-speech tags, token identity, local syntax.
  • Middle layers (5–12): Syntactic structure, phrase-level groupings, coreference.
  • Later layers: Task-specific, abstract semantic features.

The architecture explains why this gradient exists. Early layers receive representations that have undergone very little contextualization — essentially just the token and positional embeddings. They can only access local, surface-level patterns. Later layers, on the other hand, are reading from a residual stream that has already accumulated many rounds of attention and FFN processing. Each layer builds on the contextualized representations produced by all previous layers, enabling increasingly abstract structures to emerge. The depth gradient is not a design choice — it is a direct consequence of how information accumulates through residual connections.

16. Modern Improvements

The original Transformer (2017) has been refined substantially. Here are the key improvements that appear in modern LLMs, with brief explanations of why each was adopted:

Improvement What changes Why Used in
Pre-LayerNorm LN moves inside the residual branch Training stability at scale; no warm-up required GPT-2, LLaMA, Mistral
Rotary Position Embedding (RoPE) Replaces absolute pos. embeddings with rotation of Q and K Better length generalization; relative position naturally encoded at every layer LLaMA, Mistral, GPT-NeoX, Qwen
Grouped Query Attention (GQA) Multiple Q heads share a single K and V head Reduces KV cache memory at inference without meaningful accuracy loss LLaMA 2/3, Mistral
SwiGLU activation Replaces GELU in FFN with a gated linear unit: \(\text{SwiGLU}(x) = \text{Swish}(xW_1) \odot xW_2\) Consistently higher benchmark performance at equivalent parameter counts LLaMA, PaLM, Gemma
FlashAttention Reorders attention computation to minimize memory bandwidth \(O(N)\) memory instead of \(O(N^2)\); 2–4× faster; identical numerical outputs Used in most modern training stacks
RMSNorm Replaces LayerNorm with root-mean-square normalization (no mean subtraction) Simpler, ~10% faster, equivalent quality LLaMA, Mistral, Gemma
The Core Architecture Is Unchanged

Despite these refinements, the fundamental architecture described in this post remains the same. Pre-LN vs Post-LN, RoPE vs learned embeddings, SwiGLU vs GELU — these are all improvements to individual components. The overall structure (attention + FFN + residual + norm, stacked N times) has not changed since 2017.

17. Conclusion

In this post, we built the Transformer architecture from scratch — starting from the failure modes of RNNs, building the attention mechanism step by step, implementing each component in PyTorch with annotated shapes, and assembling the encoder-only, decoder-only, and encoder-decoder variants. We also traced a complete end-to-end forward pass and surveyed what trained Transformers empirically learn.

The architecture’s dominance across language, vision, speech, and biology stems from a coherent set of design choices — each solving a specific problem with a specific mechanism.

Key Takeaways

  1. Attention replaces sequential recurrence with parallel direct communication. Every token attends to every other token in a single matrix operation. No hidden state bottleneck, no sequential dependency, no vanishing gradient through time — the fundamental failures of RNNs are eliminated at the architectural level, not patched over.

  2. Q, K, V separation is intentional, not arbitrary. What a token wants (query), what it offers (key), and what it says (value) are three genuinely different roles. Separating them — as in the library lookup analogy — gives the model the flexibility to learn very different relationships for each. A single projection would conflate all three.

  3. Multi-head attention gives the model multiple simultaneous perspectives. Each head operates in its own lower-dimensional subspace and learns to track different relationship types: one head for syntax, one for coreference, one for local context. This specialization is emergent — it arises from the training signal, not from any explicit design constraint.

  4. The FFN is the knowledge store; attention is the routing system. Attention decides which tokens talk to which and mixes their representations. The FFN then transforms each token’s representation independently and nonlinearly — this is where factual associations are stored. Without the FFN, stacked attention layers collapse to a single linear transformation.

  5. Skip connections and LayerNorm make depth trainable. Residual connections create gradient highways that bypass each sublayer entirely, making it possible to train networks dozens of layers deep. Pre-LayerNorm (inside the residual branch) stabilizes training at scale without requiring learning rate warm-up.

  6. Architecture determines what tokens can see; everything else is shared. The only fundamental difference between an encoder and a decoder is the causal mask. The same attention mechanism, FFN, LayerNorm, and residual structure underlies all three variants — encoder-only, decoder-only, and encoder-decoder — differing only in which tokens each position is allowed to attend to.

The Core Architecture Is Stable

Despite years of improvements — RoPE, GQA, SwiGLU, FlashAttention, RMSNorm — the fundamental architecture described in this post has not changed since 2017. The overall structure (attention + FFN + residual + norm, stacked \(N\) times) is the same in GPT-4, LLaMA 3, and Gemini as it was in the original “Attention Is All You Need.” If you understand this post, you understand the backbone of essentially all modern AI.

What to explore next:

  • Building GPT-2 from Scratch — takes the decoder-only architecture from this post and implements a full GPT-2 training run, including mixed precision, Flash Attention, and distributed training
  • BPE Tokenizer from Scratch — implements the tokenizer that sits upstream of everything in this post
  • Tokenization Strategies — compares character, word, and subword tokenization with code examples and real model outputs

References & Resources

Back to top