Introduction

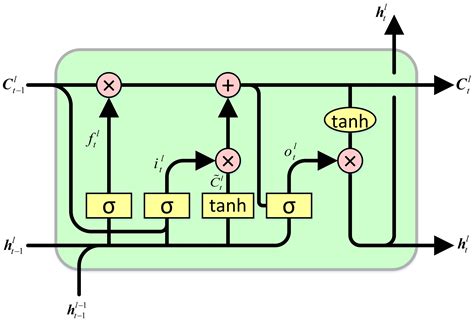
Long Short-Term Memory (LSTM) is a recurrent neural network (RNN) architectute that was introduced by Hochreiter and Schmidhuber in 1997 to solve the problem of vanishing gradients that RNNs suffered from for long sequences. This issue is the result of repeated multiplication using the same weights in all timesteps since the weights are shared between all timesteps. Instead of having one hidden state as is the case for RNNs, we have two hidden states: cell state that is responsible for retaining long short-term memory, and hidden state that is focused on predicting the next word.

RNNs and LSTMs are sequential models, which means they can only take one input at a time to produce one output because the output at time t depends not only on \(x_t\) but also on the hidden state(s) from \(t -1\). In other words, we can’t parallelize the forward pass and need to iterate over all the timesteps to get all the results.

In this post, we will focus on implementing LSTM from scratch and compare it with pytorch to check our implementation. Along the way, we will consider performance issues and some ways to optimize our implementation. Hopefully this will help us better understand LSTMs, since the only way to really understand something is to build it yourself from scratch.

Implementation

Let’s first cover, at a high level, how LSTM works:

On each timestep t, there would be two states: a hidden state \(h()\) and a cell state \(c()\)
Both are vectors length of \(n\)
The cell stores long-term information
The LSTM can read, erase, and write information from the cell. Therefore, the cell becomes more like a RAM

LSTM solves the vanishing/exploding gradients problem by making it easier to preserve information through longer timesteps.

We will first start with implementing LSTMCell that operates on 1 input at a time. Next, we will implement LSTM module that wraps the LSTMCell to work on sequence of inputs and, optionally, stack multiple layers on top of each other to increase the capacity of the model with some regularization using dropout.

LSTM Cell

Let’s take a look at the equations for an LSTMCell (each gate has the same dimension as hidden state):

\[\begin{array}{ll} \\ i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\ f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\ g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\ o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\ c_t = f_t \odot c_{t-1} + i_t \odot g_t \\ h_t = o_t \odot \tanh(c_t) \\ \end{array}\]

Where:

\(i_t\) is the input gate. It looks at \(x_t\) and \(h_t\) and determines what information to keep and what to throw away. The output is between 0 & 1 where 1 means keep all the information and 0 means get rid of this information.
\(f_t\) is the forget gate. This gate is responsible to determine which information from the old cell state needs to be forgotten in order to be replaced with new information when updating the new cell state based on the input gate.
\(g_t\) is the cell gate. This gate determines which cell elements to update with new input data.
\(o_t\) is the output gate. This is the last gate which determines which information from cell state to use to output to the new hidden state.

Even though we have 4 gates, we actually implement them using one matrix to speed up the computation. Then later we will split the output to compute the corresponding gates.

Let’s implement LSTMCell and check its correctness with pytorch.

Code

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F

# Long version
class LSTMCellNew(nn.Module):
    def __init__(self, input_sz, hidden_sz, bias=True):
        super().__init__()
        self.weight_ih = nn.Parameter(torch.randn((input_sz, hidden_sz * 4)))
        self.weight_hh = nn.Parameter(torch.randn((hidden_sz, hidden_sz * 4)))
        self.bias_ih = nn.Parameter(torch.zeros(hidden_sz * 4))
        self.bias_hh = nn.Parameter(torch.zeros(hidden_sz * 4))

    def forward(self, x, h, c):
        # T x B x hidden_sz
        out = x @ self.weight_ih + h @ self.weight_hh + self.bias_ih + self.bias_hh
        i, f, g, o = torch.split(out, 100, dim=-1)
        i, f, o = torch.sigmoid(i), torch.sigmoid(f), torch.sigmoid(o)
        g = torch.tanh(g)
        c_t = f * c + i * g
        h_t = o * torch.tanh(c_t)
        return h_t, c_t

# Short version utilizing linear layer module
class LSTMCellNew(nn.Module):
    def __init__(self, input_sz, hidden_sz, bias=True):
        super().__init__()
        self.ih = nn.Linear(input_sz, hidden_sz * 4, bias=bias)
        self.hh = nn.Linear(hidden_sz, hidden_sz * 4, bias=bias)

    def forward(self, x, h, c):
        out = self.ih(x) + self.hh(h)
        i, f, g, o = torch.split(out, 100, dim=-1)
        i, f, o = torch.sigmoid(i), torch.sigmoid(f), torch.sigmoid(o)
        g = torch.tanh(g)
        c_t = f * c + i * g
        h_t = o * torch.tanh(c_t)
        return h_t, c_t

batch_sz = 64
seq_len = 8
input_sz = 20
hidden_sz = 100
num_layers = 2

X = torch.randn(seq_len, batch_sz, input_sz, dtype=torch.float32)
c_0 = torch.randn(num_layers, batch_sz, hidden_sz, dtype=torch.float32)
h_0 = torch.randn(num_layers, batch_sz, hidden_sz, dtype=torch.float32)

pytorch_cell = nn.LSTMCell(input_sz, hidden_sz, bias=True)
(
    pytorch_cell.weight_hh.shape,
    pytorch_cell.weight_ih.shape,
    pytorch_cell.bias_ih.shape,
    pytorch_cell.bias_hh.shape,
)

(torch.Size([400, 100]),
 torch.Size([400, 20]),
 torch.Size([400]),
 torch.Size([400]))

# h: B x hidden_sz
# c: B x hidden_sz
pytorch_h, pytorch_c = pytorch_cell(X[0], (h_0[0], c_0[0]))

cell = LSTMCellNew(input_sz, hidden_sz)

# To make sure pytorch and our implementation both
# have the same weights so we can compare them
cell.ih.weight.data = pytorch_cell.weight_ih.data
cell.hh.weight.data = pytorch_cell.weight_hh.data
cell.ih.bias.data = pytorch_cell.bias_ih.data
cell.hh.bias.data = pytorch_cell.bias_hh.data

h_t, c_t = cell(X[0], h_0[0], c_0[0])

print(
    np.linalg.norm(pytorch_h.detach().numpy() - h_t.detach().numpy()),
    np.linalg.norm(pytorch_c.detach().numpy() - c_t.detach().numpy()),
)

0.0 0.0

LSTM

There are few things worth mentioning about our LSTM implementations as well as other implementations in common libraries:

We use sequence length as the first dimension instead of the batch first. This would give us better performance since we iterate over timesteps and we want to avoid copying memory for each operation which would be the case if the matrix is not contiguous when first dimension is the batch. Therefore, we use T x B x input_sz.
Backpropagation Through Time (BPTT): This essentially means we backpropagate through all the history for each example when we calculate the gradient of the loss w.r.t. weights. Since for each layer, the weights are shared among all timesteps, long sequences will suffer greatly from vanishing/exploding gradients. Therefore, we typically truncate history by detaching hidden and cell states from computation graph after every batch so gradients stop at \(t_0\) for each bach for each sequence. We only have access to the hidden/cell states from previous batch for the same sequence but can’t propagate beyond the first timestep of each batch.
We can stack LSTMs (and RNNs) on top of each other using num_layers argument. This would build multiple LSTM layers, each has its own LSTMCell that is shared across all timesteps within each layer. This would increase the capacity of the model.
When we have multilpe layers, we can either 1) iterate first over all timesteps for each layer before moving to the next layer Or 2) iterate over number of layers first for a given timestep before moving to the next timestep.
When we have long sequences, it is common that we divide the sequences into shorter segments using predefined block_size.
Since not all sequences have the same length, we need to make them of the same length to utilize matrix-matrix multiplication. There are two approaches to handle this issue:
1. Make the sequence length the length of the longest sequence. Pad shorter sequences with zeros, using either pre-padding (zeros at the beginning) or post-padding (zeros after last token at the end).
2. Padding leads to wasteful computation. To avoid this issue, we can use packed sequences where we combine all sequences together and have indices of where each sequence starts and ends.

class LSTMNew(nn.Module):
    def __init__(self, input_sz, hidden_sz, num_layers=1):
        super().__init__()
        self.num_layers = num_layers
        self.hidden_sz = hidden_sz
        self.cells = nn.ModuleList(
            [
                LSTMCellNew(input_sz, hidden_sz)
                if i == 0
                else LSTMCellNew(hidden_sz, hidden_sz)
                for i in range(self.num_layers)
            ]
        )

    def forward(self, x, h_t, c_t):
        # x  :      T     x B x hidden_sz
        # h_t: num_layers x B x hidden_sz
        # c_t: num_layers x B x hidden_sz
        T, B, _ = x.shape
        H = torch.zeros(T, B, self.hidden_sz)
        for i, cell in enumerate(self.cells):
            h, c = h_t[i], c_t[i]
            if i > 0:
                x = H
            for t in range(T):
                h, c = cell(x[t], h, c)
                H[t] = h
            # last hidden state for each layer
            h_t[i], c_t[i] = h, c
        # Truncated BPTT
        return H, (h_t.detach(), c_t.detach())

pytorch_lstm = nn.LSTM(input_sz, hidden_sz, num_layers=num_layers)
pytorch_H, (pytorch_h, pytorch_c) = pytorch_lstm(X, (h_0, c_0))

lstm = LSTMNew(input_sz, hidden_sz, num_layers=num_layers)

for i in range(num_layers):
    lstm.cells[i].ih.weight.data = getattr(pytorch_lstm, f"weight_ih_l{i}").data
    lstm.cells[i].hh.weight.data = getattr(pytorch_lstm, f"weight_hh_l{i}").data
    lstm.cells[i].ih.bias.data = getattr(pytorch_lstm, f"bias_ih_l{i}").data
    lstm.cells[i].hh.bias.data = getattr(pytorch_lstm, f"bias_hh_l{i}").data

H, (h_t, c_t) = lstm(X, h_0, c_0)

print(
    np.linalg.norm(pytorch_H.detach().numpy() - H.detach().numpy()),
    np.linalg.norm(pytorch_h.detach().numpy() - h_t.detach().numpy()),
    np.linalg.norm(pytorch_c.detach().numpy() - c_t.detach().numpy()),
)

4.6524093e-07 2.3566642e-07 4.6639343e-07

Conclusion

LSTMs were for a long time the solution for vanishing/exploding gradients problems vanilla RNNs have. They were the backbone models used in many NLP tasks such as machine translation and classification. In this post, we implemented both LSTM and LSTMCell. Hopefully, working through the implementation step by step made it a little easier and less intimidating to understand it.

The key takeaways are:

RNNs and LSTMs are sequential models. They iteratively go through tokens in the sequence, or batch of sequences, one token at a time to predict the next word. Therefore, we can’t parallelize them as we do with FNNs or CNNs.
Each timestep within the same layer shares the same weights.